数1 1章2節 因数分解
1.2次式の因数分解の公式
数1 1章1節で学習した2次式の展開公式の逆である。1つの多項式を複数の多項式または単項式の積の形で表すことを因数分解するといい、積を作っている各式のことを因数という。<公式1>の4を実際に解くときはたすき掛けを用いる。たすき掛けについては下の<補足1>に示す。
<公式1>
1.\(a^2+2ab+b^2=(a+b)^2\)
\(a^2-2ab+b^2=(a-b)^2\)
2.\(a^2-b^2=(a+b)(a-b)\)
3.\(x^2+(a+b)x+ab=(x+a)(x-b)\)
4.\(acx^2+(ad+bc)x+bd=(ax+b)(cx+d)\)
<例1>

<補足1>
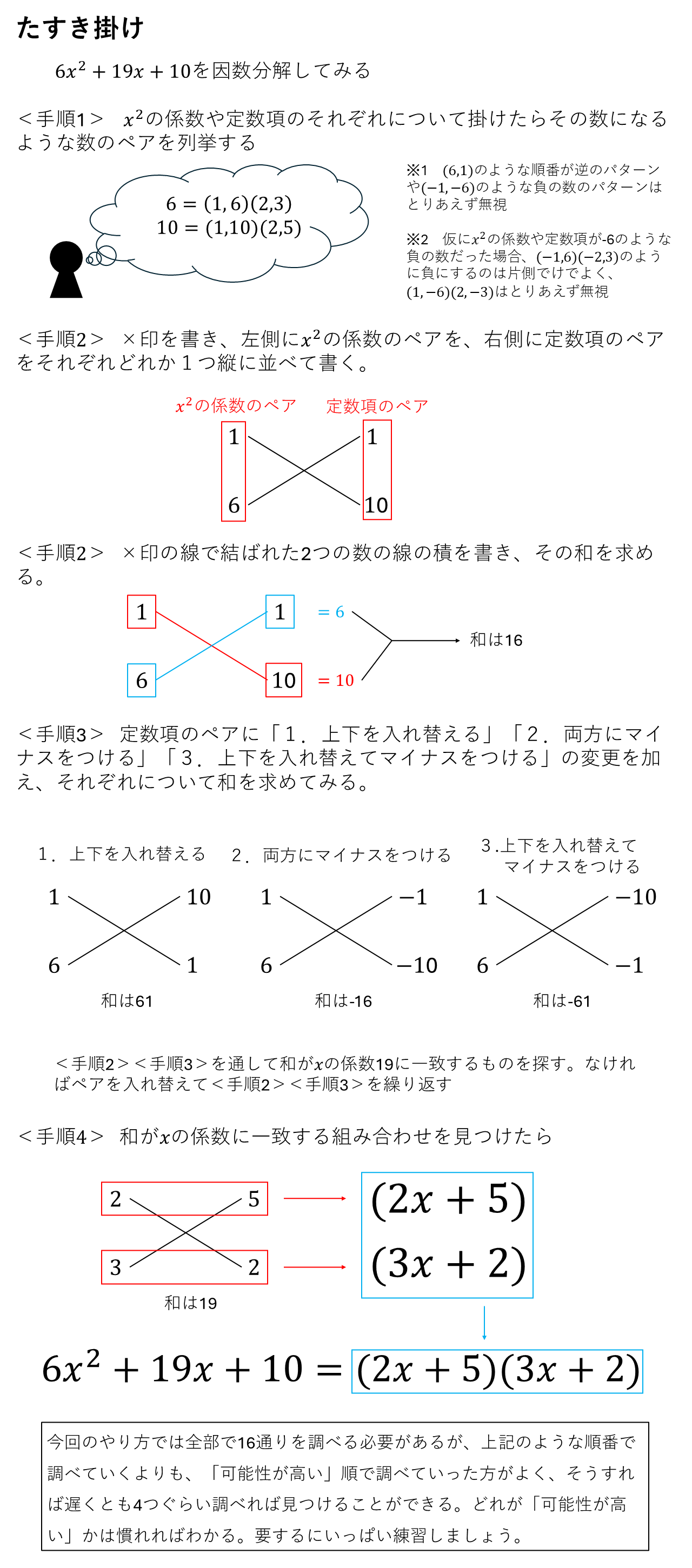
2.3次式の因数分解の公式
数1 1章1節で学習した3次式の展開公式の逆である。
<公式2>
1.\(a^3+b^3=(a+b)(a^2-ab+b^2)\)
\(a^3-b^3=(a-b)(a^2+ab+b^2)\)
2.\(a^3+3a^2b+3ab^2+b^3=(a+b)^3\)
\(a^3-3a^2b-3ab^3-b-3=(a-b)^3\)
3.知っておいたほうが良い因数分解と式変形
一度証明して確かめておくと良い。また、一般的な因数分解の手順を<補足2>に示す。
<公式3>
1.\(a^3+b^3+c^3-3abc=(a+b+c)(a^2+b^2+c^2-ab-bc-ca)\)
2.\(a^2+b^2+c^2+ab+bc+ca=\frac{1}{2}\{(a+b)^2+(b+c)^2+(c+a)^2\}\)
\(a^2+b^2+c^2-ab-bc-ca=\frac{1}{2}\{(a-b)^2+(b-c)^2+(c-a)^2\}\)
<補足2>


