数1 1章1節 多項式の加法・減法・乗法
1.単項式とその係数・次数
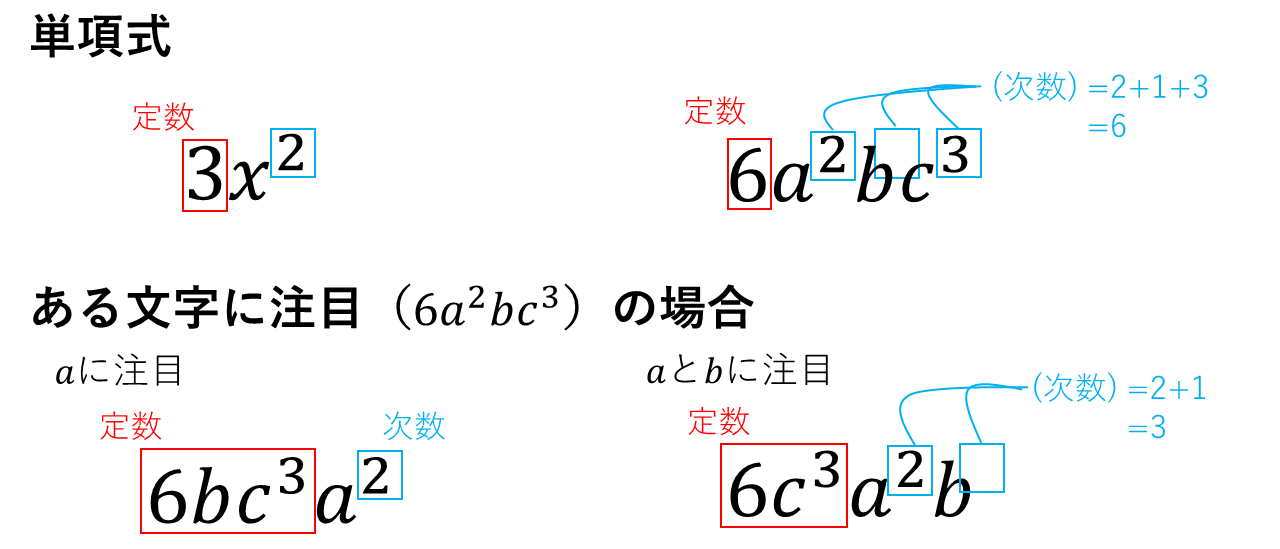
数と文字のかけ算であらわされた式を単項式という。単項式における数の部分を係数といい、文字の個数を次数という。複数の種類の文字を含んだ単項式については、ある文字に注目して次数や係数を考えることができる。このとき、次数とは注目した文字の個数を表し、係数は数と注目しなかった文字を表す。文字を含まない数(2、-10など)は定数と呼び、それだけで1つの単項式であり、その次数は0である。
<例1>
2.多項式
いくつかの単項式の和または差で表された式を多項式または整式と呼び、各単項式を項という。多項式の各項を次数が高い順に並びかえることを降べきの順に整理といい、逆に次数が低い順に並びかえることを昇べきの順に整理(あまり使わない)という。
<例2>

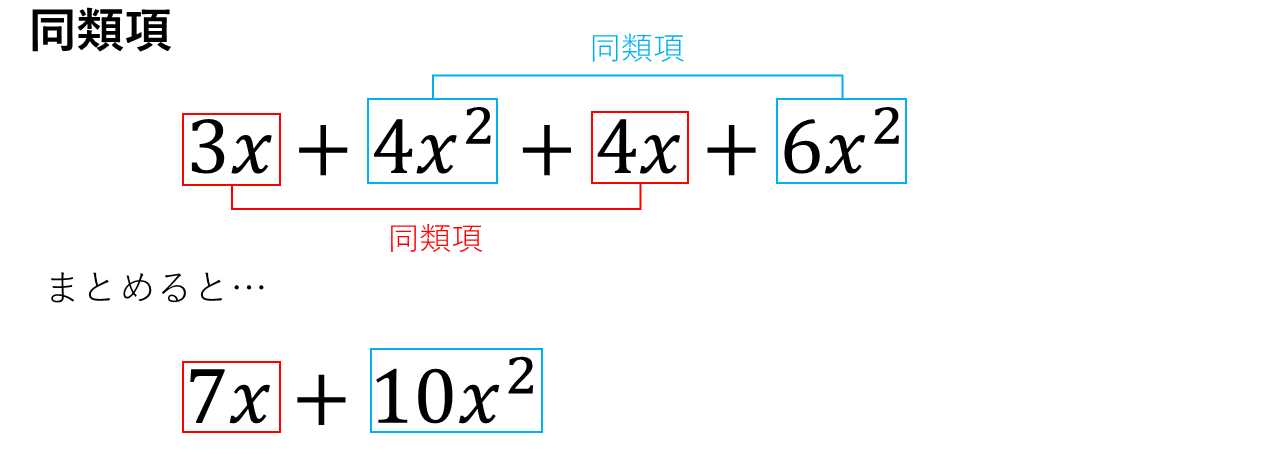
3.同類項
多項式の項のうち、文字の部分が同じ項を同類項といい、多項式は同類項をまとめて整理することができる。「式を整理する」とは一般に、同類項をまとめ、降べきの順に並びかえることをさす。
<例3>
4.多項式の次数
同類項をまとめた多項式において、もっとも次数の高い項の次数をその多項式の次数といい、次数が\(n\)の多項式を\(n\)次式という。多項式において、文字を含まない項(着目した文字があるときはその文字を含まない項)を定数項という。
<例4>
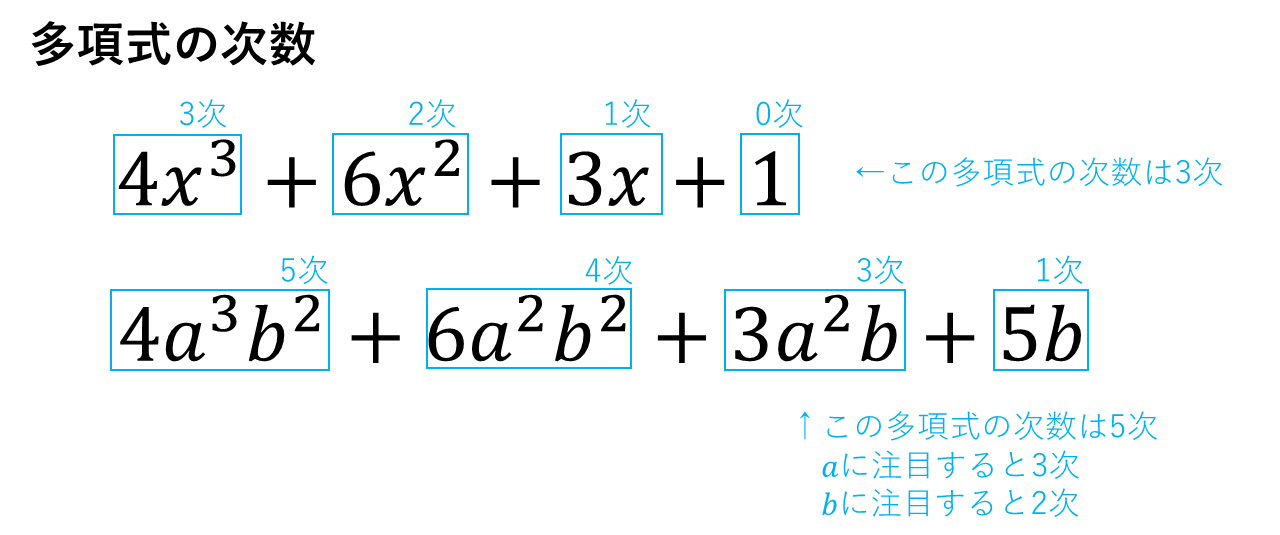
5.多項式の計算の基本公式
数字や文字で以下の3法則が成り立つことは中学数学で学習したが、式でも同様の3法則が成り立つ。
<公式1>
交換法則(加法 乗法)
\(A+B=B+A\) \(AB=BA\)
結合法則(加法 乗法)
\((A+B)+C=A+(B+C)\) \((AB)C=A(BC)\)
分配法則
\(A(B+C)=AB+AC\) \((A+B)C=AC+BC\)
<例5>

6.指数法則
<公式2>
\(m,n\)を正の整数として
1.\(x^mx^n=x^{m+n}\)
2.\((x^m)^n=x^{mn}\)
3.\((xy)^m=x^my^m\)
7.2次式の展開公式
下記の公式の1,2,3については暗記して、4については下の補足のように分配法則を用いて理解しよう。
<公式3>
1.\((a+b)^2=a^2+2ab+b^2\)
\((a-b)^2=a^2-2ab+b^2\)
2.\((a+b)(a-b)=a^2-b^2\)
3.\((x+a)(x+b)=x^2+(a+b)x+ab\)
4.\((ax+b)(cx+d)=acx^2+(ad+bc)x+bd\)
<補足1>

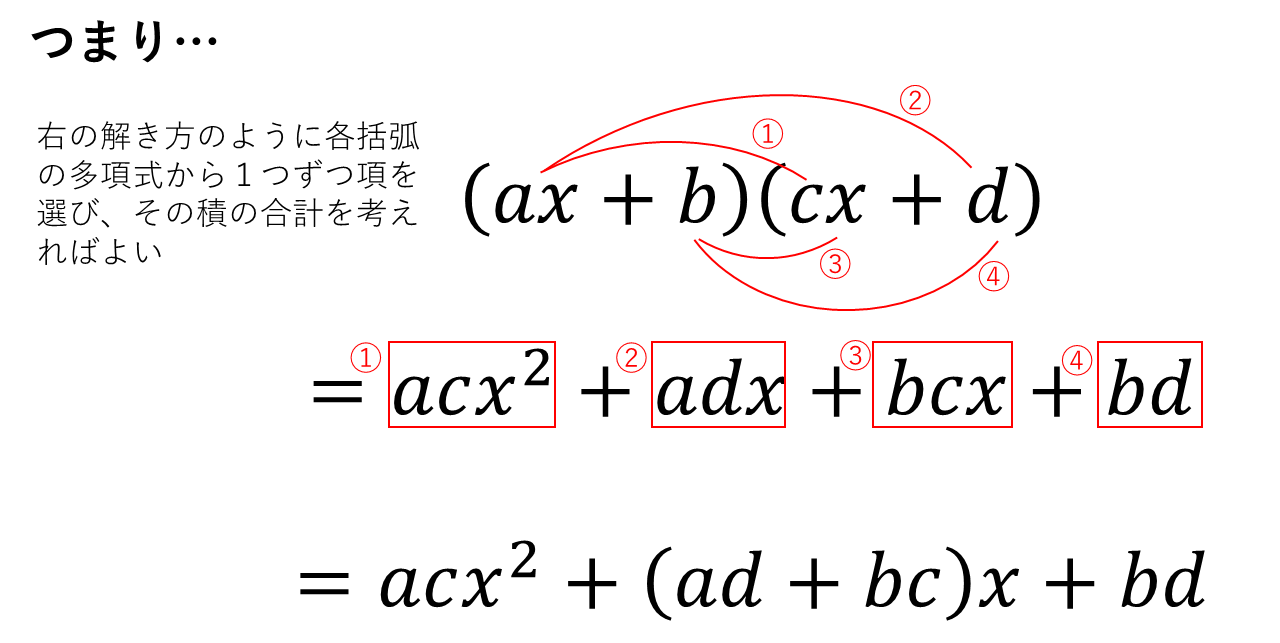


8.3次式の展開公式
覚えよう。
<公式4>
1.\((a+b)(a^2-ab+b^2)=a^3+b^3\)
\((a-b)(a^2+ab+b^2)=a^3-b^3\)
2.\((a+b)^3=a^3+3a^2b+3ab^2+b^3\)
\((a-b)^3=a^3-3a^2b+3ab^2-b^3\)
9.展開の際の工夫
展開する際の工夫としては、「公式を使えそうなところを探す」「繰り返し使われる式をまとめて考える」などが挙げられる。
<例6>



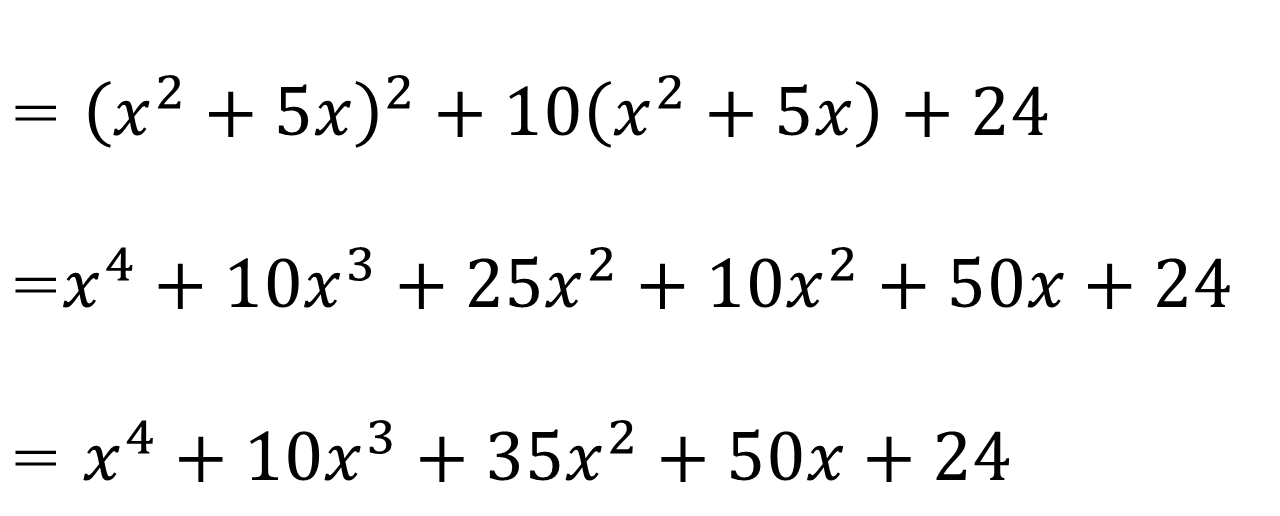
hello

