数1 1章3節　　実数

１．実数

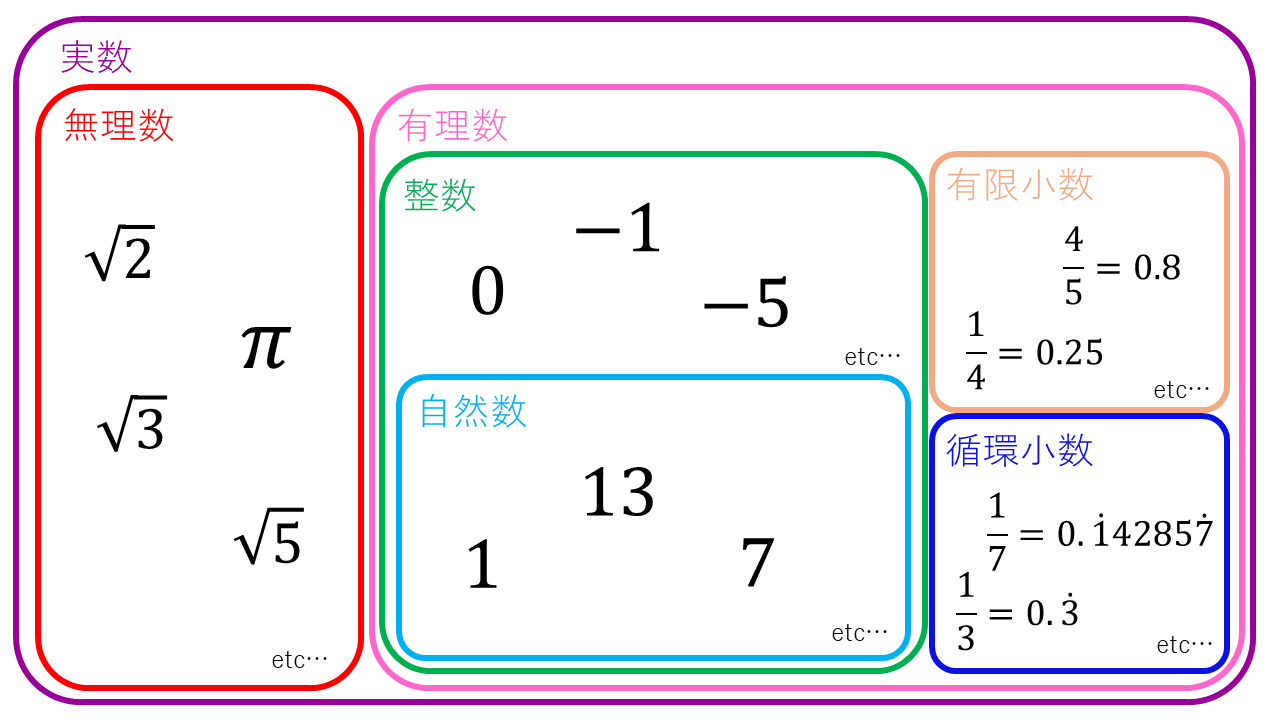
\(1,2,3\)...を自然数といい、自然数と\(0,-1,-2,-3\)...をあわせて整数と呼ぶ。
整数\(p,q\)（qは\(0\)でない）を用いて\(\dfrac{p}{q}\)とあらわされる数を有理数といい、これには整数も含まれる（\(q=1\)のとき）。有理数のうち整数でないものは、有限小数と無限小数（小数点以下の桁が無限に続く）に大別され、このうち無限小数は「例）\(\dfrac{1}{7}=0.14285714285714...\)」のように数字が循環する（例の場合「142857」が繰り返されている）。そのため、有理数の無限小数は循環小数と呼ばれている。有理数に対して、循環しない＆分数で表せない小数を無理数という。例えば、\(\sqrt{2}=1.41421356...\)や\(\pi=3.141592...\)などが挙げられるがそれらはいずれも循環しない。有理数と無理数を合わせて実数と呼ぶ。

２．絶対値

数直線上において点\(A(a)\)と原点との距離を\(a\)の絶対値といい、\(|a|\)とあらわす。つまり、\(a\)が0以上のときはそのまま外し、\(a\)が負のときは-1倍して外す。

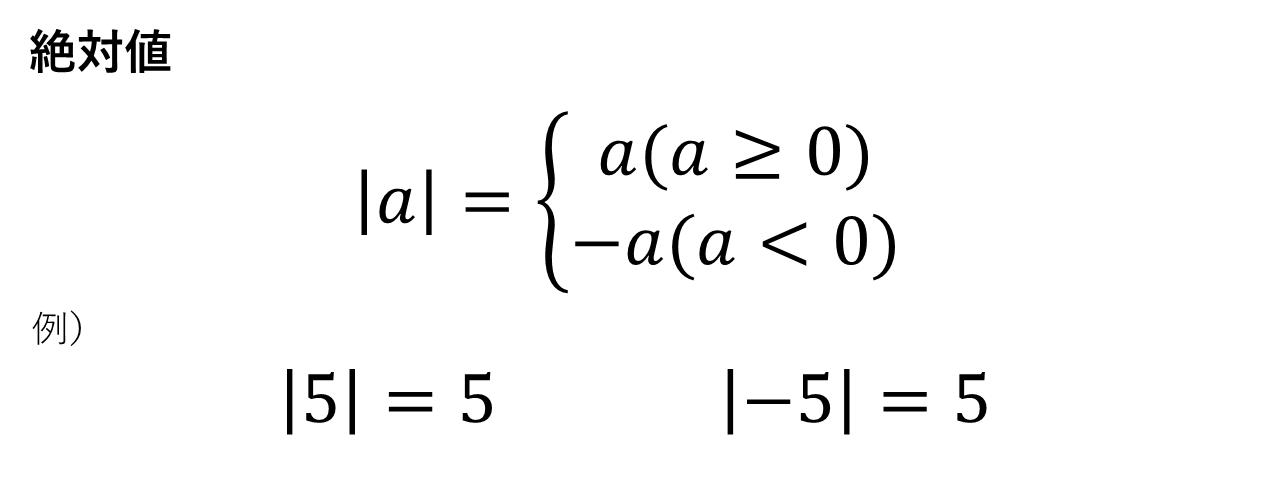
３．平方根

2乗すると\(a\)になる数を\(a\)の平方根または2乗根という。\(\sqrt{　}\)（根号）は平方根のうち正の数を表す記号であり、\(\sqrt{a}\)をルート\(a\)と読む。例えば、\(4\)の平方根は\(2\)と\(-2\)の2つであるが、\(\sqrt{4}=2\)である。